Letzte Woche stellten wir im Poker-Quiz drei Fragen rund um Flushes beim Texas-Hold’em. Diese Woche lösen wir auf, wie häufig man mit gleich- und ungleichfarbigen Karten einen Flush trifft.

Frage 1: Gleichfarbige Karten
Die Frage lautete: Wie groß ist die Wahrscheinlichkeit, mit zwei gleichfarbigen Karten (etwa J 10 ) bis zum River einen Flush in dieser Farbe zu treffen?
Um diese Frage zu beantworten, muss man ein klein wenig rechnen. Ohne Beschränkung der Allgemeinheit dürfen wir annehmen, dass wir zwei Pik-Karten haben.
Zunächst ist festzustellen, dass wir 2 Karten halten und damit noch 50 unbekannte Karten im Deck sind. Insgesamt gibt es je 13 Pik-Karten und wenn wir zwei davon haben, sind noch 11 im Deck.
Wenn mindestens drei der fünf Karten auf dem Board ebenfalls Pik sind, haben wir einen Flush. So weit, so einfach.
Die Wahrscheinlichkeit, dass genau k Karten auf dem Board eine bestimmte Farbe haben, berechnet man am einfachsten über die Hypergeometrische Verteilung.
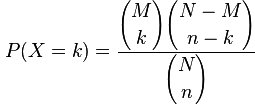
Die Formel für diese Verteilung ist rechts gegeben. Dabei sind:
k: Anzahl der Pik-Karten auf dem Board
M: Anzahl der Pik-Karten im Deck (11)
N: Anzahl aller Karten im Deck (50)
n: Anzahl aller Karten auf dem Board (5)
P(X=k): Wahrscheinlichkeit, dass genau k Pik-Karten auf dem Board liegen
Setz man jetzt für k 3, 4 und 5 ein ergibt sich:
P(X=3)=5,77%
P(X=4)=0,61%
P(X=5)=0,02%
Jetzt haben wir die Einzelwahrscheinlichkeiten dafür, dass genau 3, 4 oder 5 Pik-Karten auf dem Board kommen. Jetzt müssen wir diese Wahrscheinlichkeiten nur noch addieren und kommen auf 6,4%. Das ist genau die Wahrscheinlichkeit, dass mindestens drei Karten auf dem Board Pik sind – also die Wahrscheinlichkeit, dass wir einen Flush treffen.
6,4 Prozent – das ist nicht sonderlich viel. Das heißt , dass wir rund alle 16 Versuche mit gleichfarbigen Karten einen Flush treffen.
Frage 2: Ungleichfarbige Karten
Die Frage lautete: Wie groß ist die Wahrscheinlichkeit, mit zwei ungleichfarbigen Karten (etwa 10 5 ) bis zum River einen Flush in einer der beiden Farben zu treffen?
Wir wenden jetzt mehr oder weniger die gleiche Mathematik wie in der ersten Frage an. Ohne Beschränkung der Allgemeinheit dürfen wir annehmen, dass wir eine Herz- und eine Karo-Karte halten.
Schauen wir zunächst, unter welchen Bedingungen wir einen Herz-Flush treffen. Es sind abermals 50 unbekannte Karten im Deck, davon sind jetzt allerdings 12 in Herz (denn von den 13 Herzkarten halten wir nur eine). Wir haben diesmal nur dann einen Herz-Flush, wenn das Board 4 oder 5 Herzkarten zeigt.
In obige Formel müssen wir also für k 4 und 5 einsetzen. Dabei sind M=12, N=50 und n=5:
P(X=4)=0,888%
P(X=5)=0,037%
Damit beträgt die Wahrscheinlichkeit, dass mindestens 4 Herz-Karten kommen 0,925%.
Jetzt kann es aber ebenso passieren, dass wir einen Karo-Flush treffen. Die Berechnung dieser Wahrscheinlichkeit ist völlig symmetrisch zu der eines Herz-Flushes. Entsprechend beträgt diese Wahrscheinlichkeit auch genau 0,925%.
Zur Beantwortung der ursprünglichen Frage muss man diese beiden Einzelwahrscheinlichkeit nur noch addieren und erhält als Ergebnis 1,85%. Das ist die Wahrscheinlichkeit, dass man mit zwei ungleichfarbigen Karten einen Flush trifft.
Eine Bemerkung am Rande: Mit gleichfarbigen Karten trifft man rund 3,5 Mal so häufig einen Flush wie mit ungleichfarbigen Karten. Das ist nicht so viel häufiger, wie man intuitiv annehmen möchte und unterstreicht, dass gleichfarbige Karten in erster Linie schön aussehen, aber nur minimal besser sind als ihr ungleichfarbiges Gegenstück.
Bonus-Frage: Ein Flush auf dem Board
Zum Abschluss die Bonus-Frage. Diese lautete: Wir beobachten ein Texas-Hold’em-Spiel. Wie groß ist die Wahrscheinlichkeit, dass das Board auf dem River fünf Karten der gleichen Farbe zeigt?
Diesmal haben wir keine eigenen Karten (schließlich beobachten wir nur) und entsprechend sind noch 52 unbekannte Karten im Deck. Gehen wir zunächst der konkreteren Frage nach: Wie wahrscheinlich ist es, dass das Board einen Pik-Flush zeigt?
Insgesamt sind 13 Pik-Karten im Deck und damit gibt es 13 über 5 mögliche Boards, die 5 Pik-Karten zeigen. Das sind 1.287.
Insgesamt gibt es 52 über 5 verschiedene Boards. Das sind 2.598.960.
Das heißt nur 1.287 von 2.598.960 möglichen Boards zeigen einen Pik-Flush. Das entspricht ziemlich genau 0,05%.
Nach dem gleichen Muster sind aber auch Flushes in Herz, Karo oder Kreuz möglich. Das heißt, insgesamt gibt es 5.148 Boards, die einen Flush zeigen. Das entspricht rund 0,20% aller Boards und das ist die korrekte Antwort.
Randnotiz: Eine praktische Wette am Pokertisch
Mit anderen Worten: rund alle 500 Mal wird das Board (wenn denn bis zum River gedealt wird) einen Flush zeigen.
Das ist verdammt selten – viel seltener als die meisten Pokerspieler annehmen und damit bietet sich eine einfache, lukrative Wette am Pokertisch an:
Man offeriere seinem (mathematisch hoffentlich nicht allzu bewanderten) Nebenmann einfach Folgendes an: Wann immer das Board bis zum River gedealt wird und keinen Flush zeigt, zahlt er einen Euro. Wenn das Board jedoch einen Flush zeigt, zahlt man ihm 200 (oder gar 300) Euro. Das Angebot klingt lukrativ, ist aber für den Nebenmann langfristig ein ziemliches Verlustgeschäft.
Auflösung Gewinnspiel
Über 100 Leser haben bei unserem Gewinnspiel mitgemacht und nur 13 konnten beide Quiz-Fragen richtig beantworten. Das Los hat BigAlexMax als Sieger bestimmt. Die $15 sind auf PokerStars unterwegs.
Vielen Dank nochmals an Donk für diese Quiz-Frage.
Unser nächsten Quiz folgt in Bälde.
Dieser Artikel erschien auf PokerOlymp am 24.11.2014.

