Letzte Woche stellten wir unseren Lesern eine etwas schwierigere Frage im Poker-Quiz. Wir wollen wissen, wie (un)wahrscheinlich es ist, dass zwei Spieler in aufeinanderfolgenden WPT-Turnieren den Final-Table erreichen. Heute lösen wir die Frage auf.

Fragestellung
Bei der WPT Shootingstar nahmen vor einer Woche 708 Spieler teil. Sechs davon kamen an den Final-Table. Dabei wurde Ravee Mathi Sechster und Taylor Paur gewann.
Direkt im Anschluss fand die WPT Rolling Thunder statt. Hier meldeten sich 379 Spieler an. Mathi und Paur schafften es wieder an den sechsköpfigen Final-Table.
Wir nehmen der Einfachheit halber an, dass alle Finalisten der WPT Shootingstar auch die WPT Rolling Thunder mitspielten.
Frage: Wie wahrscheinlich ist es, dass mindestens zwei der sechs Finalisten der WPT Shooting Star auch den Final-Table der WPT Rolling Thunder erreichen?
Anmerkungen
– In der Fragestellung gehen wir der Einfachheit halber (und entgegen der WPT-Realität) davon aus, dass beide Turniere keine Re-Entry-Turniere sind.
– Wir gehen davon aus, dass alle Spieler bei den Turnieren gleich gut spielen.
– Wir wollen nicht wissen, wie wahrscheinlich es ist, dass genau Mathi und Paur den Final-Table zweimal erreichen, sondern irgendeine Kombination von mindestens zwei Finalisten des ersten Turniers.
Auflösung
Hypergeometrische Verteilung heißt das Zauberwort zur Lösung dieser (und ähnlicher) Fragen.
Man kann die Frage wie folgt vereinfachen: Von den 379 Spielern der WPT Rolling Thunder haben 6 eine besondere Eigenschaft (sie waren am FT der WPT Shootingstar). Wenn wir zufällig 6 Spieler der WPT Rolling Thunder auswählen, wie groß ist die Wahrscheinlichkeit, dass mindestens 2 von ihnen diese Eigenschaft haben?
Das ist – stochastisch gesprochen – Ziehen ohne Zurücklegen und hier greift eben die hypergeometrische Verteilung.
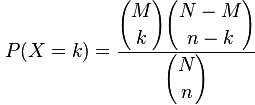
Nach der Formel rechts wird diese berechnet. Dabei sind:
k: Anzahl der WPT-Shootingstar-Finalisten am Final-Table der WPT Rolling Thunder
M: Anzahl aller WPT-Shootingstar-Finalisten (6)
N: Anzahl aller WPT-Rolling-Thunder-Spieler (379)
n: Anzahl der WPT-Rolling-Thunder-Finalisten (6)
P(X=k): Wahrscheinlichkeit, dass genau k WPT-Shootingstar-Finalisten an den Final-Table der WPT Rolling Thunder kommen.
Nun kann man die Wahrscheinlichkeiten für alle möglichen Werte von k (0 bis 6) ausrechnen:
| k | P(X=k) |
| 0 | 90,8110% |
| 1 | 8,8837% |
| 2 | 0,3009% |
| 3 | 0,0043% |
| 4 | 0,000026% |
| 5 | 0,000000057% |
| 6 | 0,000000000025% |
Wir wollten nun wissen, wie groß die Wahrscheinlichkeit für mindestens 2 identische Finalisten ist – also addieren wir alle Wahrscheinlichkeiten für k ≥ 2 zusammen.
Das macht 0,305302% – oder rund alle 332 Versuche. Das ist die richtige Lösung.
Sprich: Back-To-Back-Final-Tables von zwei Spielern sind tatsächlich sehr unwahrscheinlich, aber keineswegs unmöglich.
Mit mehr Spielern am Final-Table erhöht sich auch die Wahrscheinlichkeit ein wenig. Bei EPT-Turnieren zum Beispiel (angenommen 600 Teilnehmer, 9 Finalisten) liegt die Wahrscheinlichkeit für Back-To-Back-Final-Tables von zwei Spielern bei 0,66% oder 1 zu 150.
Bei der WSOP dürften wir dieses aber dennoch wohl nie sehen – nehmen beim Main-Event 2015 6.500 Spieler teil, liegt die Wahrscheinlichkeit, dass zwei der November-Niner von 2014 wieder an den Final-Table kommen, bei unter 0,01 Prozent (ungefähr bei 1 zu 16.000).
Auflösung Gewinnspiel
Insgesamt sechs Mitspieler kamen auf die richtige Lösung (oder zumindest in die Nähe). Wir haben alle Antworten, die gerundet 0,3% entsprachen als korrekt betrachtet. Das Los hat Superman1660 als Sieger bestimmt und die 15 Dollar sind auf PokerStars unterwegs.
Vielen Dank an alle Mitspieler und unser nächstes Quiz folgt in Bälde.
Dieser Artikel erschien auf PokerOlymp am 23.03.2015.


