Die Begriffe Glück und Pech sind untrennbar mit dem Pokerspiel verbunden. Welchen Einfluss haben diese Aspekte tatsächlich? Wie lange muss man spielen, um Glück und Pech zu nivellieren?Gewinnraten, Statistiken und Downswings
Weitere Artikel der Serie
» Erwartete und tatsächliche Gewinne beim No-Limit-Poker
» Erwartete und tatsächliche Gewinne bei Sit-and-Gos
» Häufigkeit von Downswings
» PokerOlymp-Varianz-Rechner
“Spätestens nach einer Millionen Händen haben sich Glück und Pech ausgeglichen”, meinte einer meiner Kollege diese Woche. Dem ist mitnichten so! Bei einem Spieler mit einer durchschnittlichen Gewinnrate spielt die Varianz – Glück und Pech – auch nach so vielen Händen noch eine bedeutende Rolle. Diese Artikelserie soll sich dem Phänomen der Varianz beim Pokerspiel mathematisch nähern und dieser Artikel wird die These, dass selbst eine Millionen Hände die Varianz nicht nivellieren untermauern.
Im ersten Teil werde ich kurz auf die mathematischen Eigenschaften der Gewinnrate beim Poker eingehen. Anhand von zwei Beispielen werden diese Eigenschaften mit Leben gefüllt und es wird sich zeigen, dass Glück und Pech auch über einen vergleichsweise langen Spielzeitraum eine signifikante Rolle spielen.
Im Folgenden gehe ich ausschließlich von No-Limit-Poker aus. Die Überlegungen lassen sich zwar auch auf andere Varianten übertragen, aber insbesondere für Turniere und Sit-and-Gos werden sich andere Ergebnisse ergeben.
Kenngrößen der Gewinnrate
Die Gewinnrate beim Poker hat einen gewissen Erwartungswert (µ) – dieser wird in der Regel in Big Blinds pro 100 Hände angegeben. So bedeutet zum Beispiel die Angabe µ=5BB/100, dass ein Spieler im Schnitt 5 Big Blinds auf 100 Hände gewinnt.
Eine weitere wichtige Kenngröße der Gewinnrate die Standardabweichung (σ). Diese gibt an, wie sehr die tatsächliche Gewinnrate im Schnitt vom Erwartungswert abweicht. Platt formuliert: Ein aggressiver Spieler hat viele Swings, in den meisten Sessions gewinnt er entweder sehr viel oder verliert sehr viel. Seine Standardabweichung ist hoch. Ein tighter Spieler hingegen hat viel weniger Swings. Seine Standabweichung ist entsprechend niedriger.Die Standardabweichung wird ebenfalls in Big Blinds pro 100 Hände angegeben.Beim No-Limit-Texas-Hold’em mit 100BB Stacks kann man von einer Standardabweichung zwischen 50 und 100 BB ausgehen (ausgenommen Heads-Up-Spiele).
Gewinnraten über einen langen Zeitraum
Um Gewinnraten über einen langen Zeitraum zu simulieren, zu testen oder um bestimmte Aussagen über sie zu treffen, ist die höhere Mathematik sehr hilfreich.
Konkret hilfreich ist der zentrale Grenzwertsatz1, der – grob gesprochen – besagt, dass sich Gewinnerwartung und Verteilung über einen hinreichend langen Zeitraum normalverteilt verhalten. Die Normalverteilung ist eine statistische Verteilung, die sich ausschließlich über Erwartungswert und Standardabweichung definiert. Ergo: Zum Beschreiben und Untersuchen der Gewinnerwartung über einen langen Zeitraum benötigt man nur diese zwei Kenngrößen.
Im Folgenden geht dieser Artikel davon aus, dass die Gewinnverteilung eines Spielers normalverteilt ist2.
Beispiel 1: Ein Spieler mit einer Gewinnrate von 5BB/100
Schauen wir uns zunächst einen durchaus erfolgreichen Spieler an. Er weiß, dass er auf seinem Limit eine Gewinnrate von 5 Big Blinds auf 100 Hände hat. Er hat eine Standardabweichung von 70 Big Blinds auf 100 Hände. Eine solche Standardabweichung ist für Full-Ring-Tische üblich und liegt auch in der Größenordnung von halbwegs tighten 6-max Spielern.
Erwarteter Gewinn
Angenommen, dieser Spieler nimmt sich nun vor, während der nächsten Wochen oder Monate 200.000 Hände zu spielen und fragt sich, welchen Gewinn er erwarten kann. Diese Frage zu beantworten ist leicht: Sein erwarteter Gewinn beläuft sich auf 5BB/(100Hände) * 200.000Hände, also 10.000BB.
Die viel spannendere Frage jedoch ist: Wie sicher kann er eigentlich sein, dass sein Gewinn tatsächlich in dieser Größenordnung ist?
Standardabweichung
Seine Standardabweichung beläuft sich über diesen Zeitraum auf Wurzel(200.000/100) * 70BB, also rund 3.130BB. Im Gegensatz zum Erwartungswert erhöht sich die Standardabweichung nicht linear, sondern nur in Form einer Wurzel3.
Dies bedeutet, der Spieler kann davon ausgehen, dass er nach 200.000 Händen seinen erwarteten Gewinn in Höhe von 10.000 Big Blinds im Schnitt um 3.130 Big Blinds verfehlen (oder übertreffen) wird.
Der Spieler wird also wahrscheinlich nicht genau 10.000 Big Blinds gewinnen, sondern eher deutlich mehr oder weniger. Wie sehr sein tatsächlicher Gewinn abweichen wird, lässt sich noch etwas genauer beantworten.
Konfidenzintervalle
Die Wahrscheinlichkeit, dass sein tatsächlicher Gewinn um weniger als eine Standardabweichung vom erwarteten Gewinn abweicht, liegt bei 70 Prozent.Die Wahrscheinlichkeit, dass sein tatsächlicher Gewinn um weniger als zwei Standardabweichungen vom erwarteten Gewinn abweicht, liegt bei 95 Prozent4.
Mit anderen Worten: in 95% der Fälle wird unser Spieler im konkreten Beispiel nach 200.000 Händen zwischen 10.000 – 3.130 * 2 BB und 10.000 + 3.130 * 2 BB, also zwischen 3.740BB und 16.260BB gewonnen haben. Dieses nennt man auch das 95%-Konfidenzintervall. Dieses beschreibt, worauf sich der Spieler realistischerweise gefasst machen muss.
Schon anhand dieser Zahlen sieht man eines: 200.000 Hände sind nicht sonderlich viel! Der Spieler muss sich darauf einstellen, einen Betrag zwischen unter 40 Stacks oder über 160 Stacks zu gewinnen.
Das folgende Diagramm verdeutlicht diese Werte. Auf der X-Achse sind die gespielten Hände dargestellt, die blaue Linie zeigt den erwarteten Gewinn an, die rote Linie die Standardabweichung. Orange und Grüne Linie sind die obere bzw. untere Grenze des 95%-Konfidenzintervalls.
Diagramm eines Spielers mit einer Gewinnrate von 5BB/100 und einer Standardabweichung von 70BB/100. (200.000 Hände)
Erst nach knapp 80.000 Händen liegt das 95%-Konfidenzintervall komplett über Null. Das heißt für einen Zeitraum von weniger Händen ist die Wahrscheinlichkeit, dass der Spieler – obwohl er eine positive Gewinnrate hat – Verlust macht, vergleichsweise hoch.
Länger spielen!
Angenommen, unser Spieler entschließt sich aufgrund der ihm bevorstehenden Varianz, nicht nur 200.000 Hände zu spielen, sondern gleich eine Million. Ein hohes Spielvolumen schlägt der Varianz tatsächlich ein Schnippchen, wie das folgende Diagramm zeigt. Es ist das selbe wie obiges, nur auf der X-Achse verlängert.
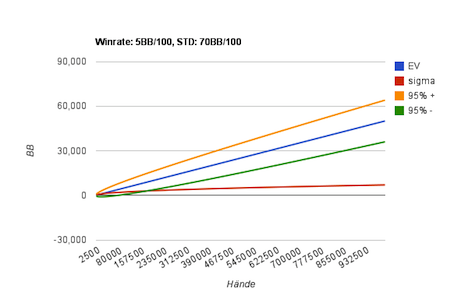
Diagramm eines Spielers mit einer Gewinnrate von 5BB/100 und einer Standardabweichung von 70BB/100. (1.000.000 Hände)
Hier zeigt sich sehr deutlich, dass der Spieler tatsächlich erwarten kann, die Varianz ein wenig auszutricksen.
Sein erwarteter Gewinn liegt bei 50.000BB, das 95%-Konfidenzintervall liegt zwischen 36.000BB und 64.000BB. Das heißt, unser Spieler kann davon ausgehen, dass er mit sehr großer Wahrscheinlichkeit wenigstens 360 Stacks nach einer Millionen Händen gewonnen haben wird.
Aber es zeigt sich auch: die realisierte Gewinnrate liegt irgendwo zwischen 3,6BB/100 und 6,4BB/100. Eine Millionen Hände reichen also auch noch nicht aus, wirklich verlässliche Angaben über Gewinnraten zu machen.
Beispiel 2: Ein Spieler mit einer Gewinnrate von 3BB/100
Ein zweites Beispiel soll den Dämon Varianz in all seiner Mächtigkeit darstellen. Diesmal greifen wir uns einen Spieler, der eine etwas niedrigere Gewinnrate hat. Er gewinnt im Schnitt 3BB pro100 Hände, hat aber die gleiche Standardabweichung in Höhe von 70BB pro 100 Hände.
Sein erwarteter Gewinn über 200.000 Hände liegt bei 6.000 Big Blinds, seine Standardabweichung (ebenso wie beim vorigen, besseren Spieler) bei 3.130 Big Blinds und damit liegt sein 95% Konfidenzintervall zwischen -260 Big Blinds und +12.260 Big Blinds.Der Spieler kann also nach 200.000 Händen noch nicht einmal sicher sein, dass er überhaupt Gewinn macht.
So sieht das dazugehörige Diagramm aus:
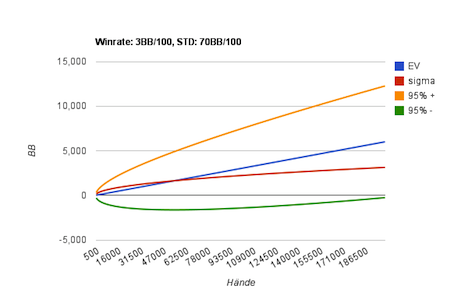
Diagramm eines Spielers mit einer Gewinnrate von 3BB/100 und einer Standardabweichung von 70BB/100. (200.000 Hände)
Mehr spielen, hilft jedoch auch diesem Spieler. Grindet dieser Spieler eine Millionen Hände, liegt sein erwarteter Gewinn bei 30.000BB. Sein 95%-Konfidenzintervall jedoch klafft immer noch weit auf. Es liegt zwischen 16.000BB und 44.000BB. Das ist ein Unterschied von einem Faktor, der fast 3 beträgt!
So sieht das Diagramm nach einer Millionen Hände aus:
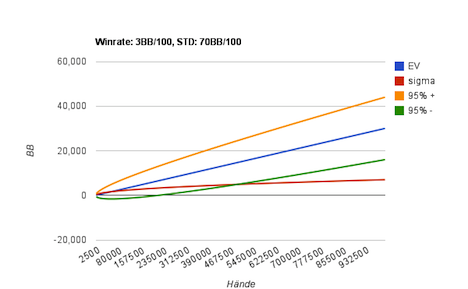
Diagramm eines Spielers mit einer Gewinnrate von 3BB/100 und einer Standardabweichung von 70BB/100. (1.000.000 Hände)
Bisherige Ergebnisse
Soweit hat dieser Artikel gezeigt, dass es einer sehr formidablen Anzahl gespielter Hände bedarf, um sich seiner Gewinnrate anzunähern und die Varianz aus dem Endergebnis zu tilgen. Je niedriger die Gewinnrate eines Spielers ist, desto schlimmer schlägt die Varianz zu buche.
Verlustreiche Sessions sind bei jedem Spieler statistisch vorprogrammiert. Es ist wichtig, dies immer im Hinterkopf zu haben und nicht sofort die Pokerkarriere an den Nagel hängen zu wollen, nur weil die letzten zehn- oder zwanzigtausend Hände schlecht liefen.
Aber der Artikel zeigt auch, dass Ausschläge in die Positive Richtung ebenso vorprogrammiert sind. Tatsächlich kann es passieren, dass ein Spieler, der im Schnitt 3 Big Blinds auf 100 Hände verliert, nach 200.000 Händen noch im Plus ist. Die beobachtete Gewinnrate entspricht eben erst nach deutlich mehr Händen der tatsächlichen Gewinnrate!
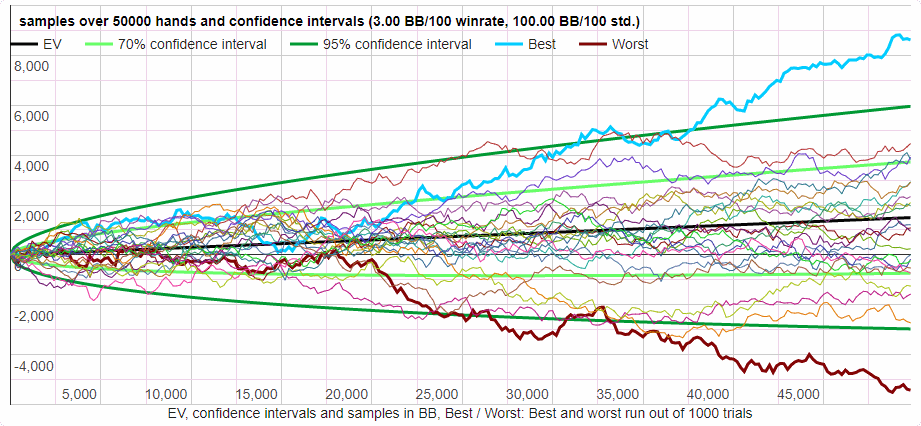
Das folgende Diagramm zeigt zum Abschluss eine Gewinnsimulation von elf Spielern. Alle spielen identisch und haben eine Gewinnrate von 5BB/100. Das Einzige, was sie während des Spiels von 200.000 Händen unterscheidet ist Glück oder Pech.
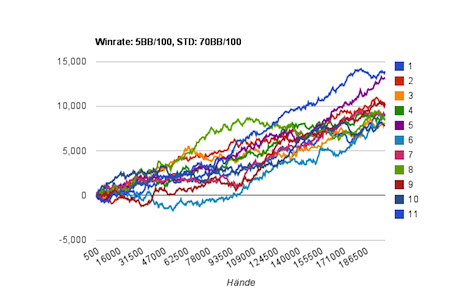
Simulation von elf Spielern mit einer Gewinnrate von 3 BB/100 und einer Standardabweichung von 70BB/100. (200.000 Hände)
Am Ende landen alle im 95%-Konfidenzintervall, aber sie verteilen sich in diesem Intervall breit gefächert und der arme Spieler Nummer 6 war während der ersten 100.000 Hände fast durchgehend in den Miesen.
In den nächsten Artikeln der Serie werde ich auf Downswings, die Ursachen der Varianz beim Poker und auf die Frage, wie man seine eigene Gewinnrate überhaupt ermittelt, eingehen.
1Zentraler Grenzwertsatz in der Wikipedia
2 Diese Annahme ist trotz des zentralen Grenzwertsatzes sehr stark. Tatsächlich sind die Gewinnverteilungen beim No-Limit-Poker erst bei einer Stichprobengröße von mehreren zehntausend, besser noch hunderttausend Händen normalverteilt. Bei kleineren Stichproben unterschätzt die Normalverteilung die Heavy Tails (hohe 4. Momente) der tatsächlichen Gewinnverteilung.
3 Bezüglich Details zu diesem Sachverhalt sei auf den Wikipedia Artikel zur Standardabweichung verwiesen.
4 Diese Eigenschaften leiten sich aus den Eigenschaften der Normalverteilung ab. Siehe Konfidenzintervall bei Wikipedia.
Dieser Artikel erschien auf PokerOlymp am 18.02.2011.
Autor: Arved Klöhn.


Was für ein Scheiß!