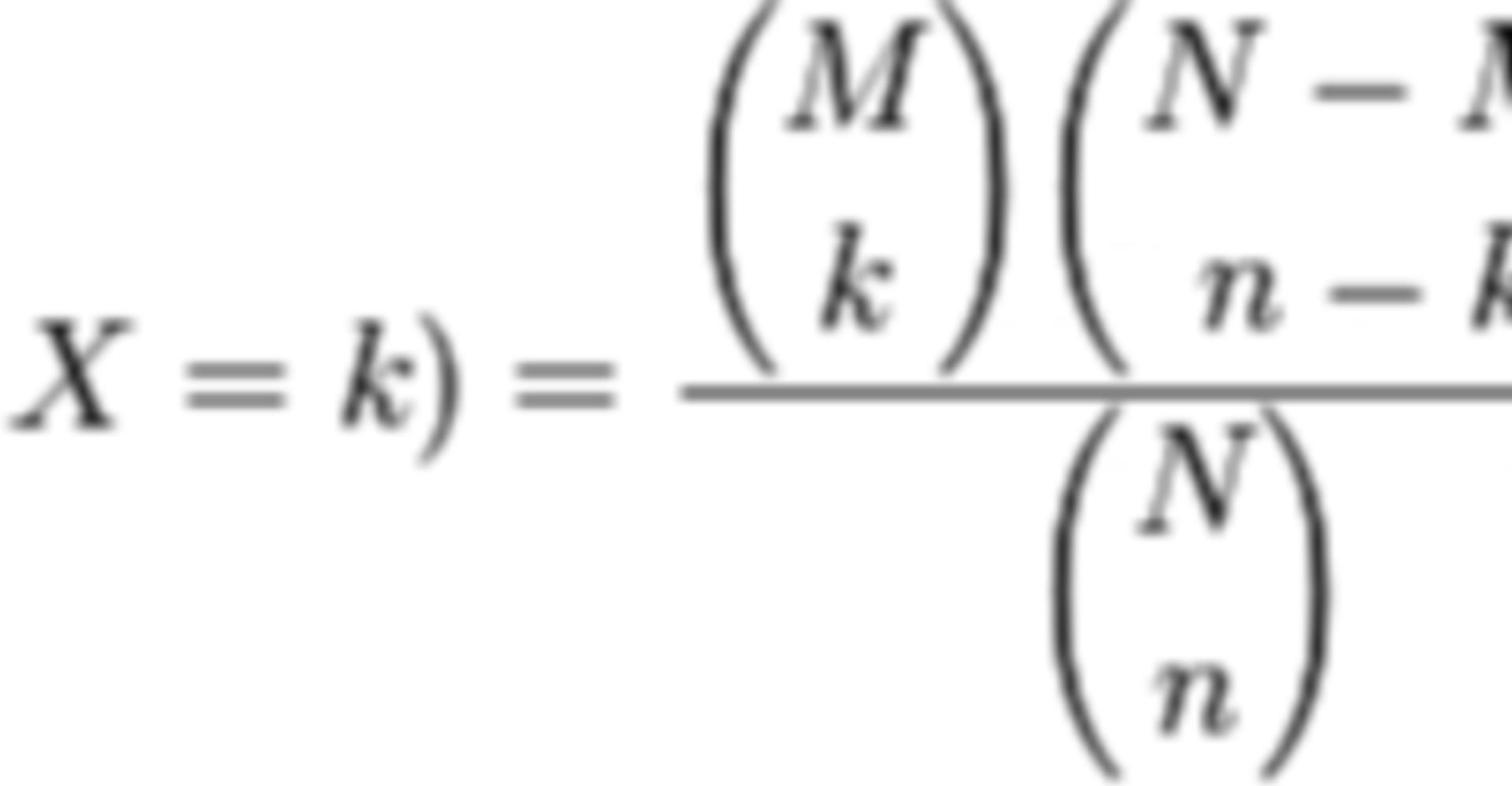Zum Wochenende stellten wir unseren Lesern eine einfache Ja-Nein-Frage zur Verteilung von Assen im Kartendeck. Hier lösen wir diese Quizrunde auf und erklären die etwas verblüffende Antwort.
.png)
Die Frage: Verteilung von Assen im Homegame
Zunächst noch einmal die Frage:
Während einer Pause in einer Home-Game-Runde entspannt sich zwischen Aida und Jochen eine angeregte Diskussion über Wahrscheinlichkeiten beim Pokern und beim Kartenspielen im Allgemeinen.
Schließlich kommen die beiden darauf zu sprechen, wo sich statistisch gesehen wohl die Asse in einem Kartendeck verstecken. Jochen meint, dass die Asse gleichmäßig im Deck verteilt sind, Aida meint, die Asse sind eher weiter vorne zu finden.
Aida ist sich ihrer Sache so sicher, dass sie Jochen sogar eine Wette anbietet: "Nimm einfach mal die ersten 20 Karten vom Deck. Ich gewinne die Wette, wenn mindestens zwei Asse dabei sind. Wenn nicht, gewinnst Du."
Die Frage nun lautet: Sollte Jochen diese Wette annehmen?
Auflösung
Die Lösung vorweg: Jochen sollte die Wette nicht annehmen. Die Wahrscheinlichkeit, dass unter den ersten 20 Karten mindestens zwei Asse sind, liegt bei etwas über 50 Prozent und die Wette ist nicht ganz fair für ihn.
Das klingt zunächst wenig plausibel – Unter den ersten 20 Karten sollen mit einer Wahrscheinlichkeit von mehr als 50% mindestens zwei Asse sein?
Müssen dafür statistisch gesehen in den ersten 20 Karten nicht mehr Asse sein als in den letzten 32 Karten?
Nein, müssen nicht und die mangelnde Plausibilität der Antwort liegt in der Interpretation der Fragestellung begründet.
Am einfachsten sieht man das ein, wenn man bedenkt, dass Jochen die Wette nur gewinnt, wenn unter den ersten 20 Karten nur eines oder gar kein Ass ist. Aida gewinnt hingegen, wenn es 2, 3 oder 4 Asse sind.
Die genaue Lösung
Die genaue Wahrscheinlichkeit ermittelt man am einfachsten über das Ziehen ohne Zurücklegen und die Hypergeometrische Verteilung:
Nach der Formel rechts wird diese berechnet. Dabei sind:
k: Anzahl der gezogenen Asse
M: Anzahl der Asse im Deck (4)
N: Anzahl aller Karten im Deck (52)
n: Anzahl der gezogenen Karten
P(X=k): Wahrscheinlichkeit, dass genau k Asse unter den ersten n gezogenen Karten sind.
Wir haben das hier mal für ein paar n und alle k durchgerechnet.
| Gezogene Karten | Kein Ass | 1 Ass | 2 Asse | 3 Asse | 4 Asse | Min. 2 Asse |
|---|---|---|---|---|---|---|
| 5 | 65,9% | 29,9% | 4,0% | 0,2% | 0,0% | 4,2% |
| 10 | 41,3% | 42,4% | 14,3% | 1,9% | 0,1% | 16,3% |
| 15 | 24,4% | 43,1% | 25,8% | 6,2% | 0,5% | 32,6% |
| 20 | 13,3% | 36,6% | 34,8% | 13,5% | 1,8% | 50,1% |
| 25 | 6,5% | 27,0% | 38,9% | 22,9% | 4,7% | 66,5% |
| 26 | 5,5% | 25,0% | 39,0% | 25,0% | 5,5% | 69,5% |
| 30 | 2,7% | 17,1% | 37,1% | 33,0% | 10,1% | 80,2% |
| 35 | 0,9% | 8,8% | 29,9% | 41,1% | 19,3% | 90,3% |
| 40 | 0,2% | 3,3% | 19,0% | 43,8% | 33,8% | 96,6% |
| 45 | 0,0% | 0,6% | 7,7% | 36,7% | 55,0% | 99,4% |
Es zeigt sich: Bei 20 gezogenen Karten liegt die Wahrscheinlichkeit, bereits 2, 3 oder 4 Asse erwischt zu haben bei 50,1 Prozent. Die Wahrscheinlichkeit für das Gegenereignis (nur ein oder gar kein Ass zu ziehen) liegt bei 49,9 Prozent.
Ganz deutlich wird es bei 26 gezogenen Karten, der Hälfte des Decks. Hier beträgt die Wahrscheinlichkeit, mindestens zwei Asse gezogen zu haben, bereits fast 70 Prozent. Die Wahrscheinlichkeit höchstens zwei Asse zu ziehen beträgt übrigens bei 26 Karten genauso viel, auch fast 70 Prozent. Das ist allerdings kein Widerspruch, denn der Fall genau zwei Asse ziehen kommt bei beiden Ereignissen vor.
Auflösung Gewinnspiel
Tatsächlich hatten nur rund 40% aller Einsendungen die richtige Lösung getippt – ganz so leicht war die Frage dann wohl doch nicht.
Das Los hat von Seis als Sieger bestimmt. Er hatte sich sogar die Mühe gemacht, dass alles zweimal durchzurechnen. Beide Male viel zu umständlich, aber beim zweiten Mal richtig. Die 15 Dollar sind auf PokerStars unterwegs.
Unser nächstes Gewinnspiel folgt sicherlich in Bälde.
Dieser Artikel erschien auf PokerOlymp am 22.07.2015.