Lohnt sich Manipulation beim Online-Poker für den Anbieter? Wie lange könnte man Betrug statistisch überhaupt verbergen?

Dieser Artikel soll an anhand eines reichlich simplen Spiels klären, ob sich Manipulationen beim Online-Poker für den Anbieter überhaupt auszahlen, oder ob der Anbieter nicht wesentlich bessere Einnahme-Möglichkeiten hat.
Nachdem ich in den vergangenen Tagen ein paar Posts im größten Online-Poker-Ist-Rigged-Thread im 2+2-Forum, englisch quergelesen habe, stellte sich mir die Frage, wie sehr man eigentlich bei einem Spiel betrügen darf, ohne dass die Mitspieler misstrauisch werden, weil sie zu viel Geld verlieren.
Um dieser Frage nachzugehen, weiche ich auf ein ganz einfaches Spiel aus und versuche mich darin, dieses Spiel so zu gestalten, dass ich durch Manipulation eine möglichst große Menge Geld verdiene.
Das Münzwurf-Spiel
Im folgenden will ich ein denkbar einfaches Spiel betrachten: Ich biete einem Spieler einen Münzwurf an, fällt die Münze auf “Kopf”, gewinne ich einen Euro, fällt die Münze auf “Zahl”, gewinnt der Spieler einen Euro. Dieses Spiel wiederhole ich so lange, bis der Spieler keine Lust mehr hat.
Nun ist klar, dass ich mit diesem Spiel kein Geld verdienen kann, wenn ich dieses Spiel mit einer fairen Münze betreibe. Langfristig werden sich Kopf und Zahl ausgleichen und ich habe keinen Vorteil.
Um mir einen Vorteil zu verschaffen, modifiziere ich das Spiel ein wenig, ohne es meinem Gegner zu sagen: ich streue zwischendurch einfach Würfe mit einer manipulierten Münze ein, die unter Garantie Kopf zeigen wird.
Nun werde ich langfristig Gewinn machen, denn ich werde, jedes Mal, wenn ich mit der manipulierten Münze werfe, einen Euro verdienen. Wie viel ich verdiene, hängt nur davon ab, wie häufig ich mit der manipulierten anstatt einer fairen Münze werfe.
Der offensichtliche Betrug

Angenommen, ich fühle mich besonders raffgierig, und werfe bei jedem zweiten Wurf mit der manipulierten Münze. Dann werde ich langfristig in 75 Prozent aller Würfe Kopf werfen (in 50 Prozent der Fälle automatisch durch die manipulierte Münze und in den anderen 50 Prozent der Fälle hat mein Gegenüber immerhin noch eine 50/50-Chance auf Zahl).
Die Frage ist nun, wie lange kann ich dieses Spiel machen, bevor mein Gegner misstrauisch wird.
Nach 8 Würfen zum Beispiel hat mein Gegenüber im Schnitt 2 Mal Zahl getroffen – etwas zu wenig, aber das klingt noch nicht sonderlich misstrauenserweckend. Wiederhole ich das Spiel aber nun 40 Mal, sieht das Ergebnis schon frappierender aus – ich habe im Schnitt 30 Mal Kopf getroffen, mein Gegenüber aber nur 10 Mal Zahl. Die Wahrscheinlichkeit, dass man mit einer fairen Münze nach 40 Würfen 10 Mal oder seltener Zahl trifft, liegt bei rund 0,1% – oder rund eins zu tausend1.
Hier wird es schon schwierig, mein Gegenüber noch davon zu überzeugen, dass er einfach nur Pech hat. Spätestens nach 100 Würfen dürfte der Spieler dann vollends überzeugt sein, über den Tisch gezogen zu werden. Denn dann hat er im Schnitt nur 25 Mal Zahl getroffen. Die Wahrscheinlichkeit, dass er mit einer fairen Münze so selten Zahl trifft, liegt bei 0,000028%, oder rund 1 zu 3,5 Millionen.
Spätestens nach 100 Würfen dürfte dieser Spieler mir also davon laufen, andere vor meinem Spiel warnen, meine Geschäftsidee wäre zunichte gemacht und womöglich würde ich mich noch wegen Betruges verantworten müssen.
Ich hätte während dieser 100 Würfe zwar im Schnitt 50 Euro verdient, aber sonderlich lohnenswert erscheint mir dies nicht.
Der weniger offensichtliche Betrug
Gut, womöglich bin ich zu gierig, wenn ich gleich jeden zweiten Wurf manipuliere. Wie würde sich das Spiel verändern, wenn ich nur bei jedem zehnten Wurf zur manipulierten Münze greife?
Klar, meine Gewinnmarge wäre kleiner, aber meine Mitspieler würden nicht so schnell misstrauisch. Nach 100 Würfen zum Beispiel hätte mein Gegenüber im Schnitt nun 45 Mal Zahl getroffen – die Wahrscheinlichkeit, dass dies mit einer fairen Münze passiert, liegt bei über 18 Prozent. Das sieht glaubwürdig aus.
Was passiert aber nun, wenn mein Gegenüber länger spielt? Nach 1.000 Würfen hätte er im Schnitt nur 450 Mal Zahl getroffen. Die Wahrscheinlichkeit für einen derart schlechten Lauf mit einer fairen Münze, liegt bei rund 0,1 Prozent – schon wieder hätte mein Gegenüber Grund, misstrauisch zu werden.
Spätestens nach 3.000 Würfen würde mein Betrug wieder so offensichtlich werden, dass ich mein Geschäft abbrechen müsste. Dann hätte mein Gegenüber im Schnitt nur 1.350 Mal Zahl getroffen (150 Mal weniger als mit einer fairen Münze) – die Wahrscheinlichkeit für einen so schlechten Lauf liegt bei 0,0000022% – etwa 1 zu 46 Millionen.
Nach 3.000 Würfen hätte ich im Schnitt immerhin 300 Euro durch meinen Betrug verdient, aber nach einer validen Geschäftsidee sieht das immer noch nicht aus.
Der versteckte Betrug

Offensichtlich kann ich umso länger unentdeckt betrügen, je weniger offensichtlich mein Betrug ist. Manipuliere ich jeden zweiten Wurf, fliege ich nach spätestens 100 Würfen auf und habe maximal 50 Euro verdient. Manipuliere ich nur noch jeden zehnten Wurf, fliege ich erst nach 3.000 Würfen auf und habe schon 300 Euro verdient.
Gehe ich doch also gleich einen ganz großen Schritt weiter – ich manipuliere nur noch jeden tausendsten Wurf. Hier würde mein Betrug selbst nach einer Million Würfe nicht auffallen – mein Gegenüber hätte im Schnitt 499.500 Mal Zahl getroffen, 500 Mal zu wenig. Die Wahrscheinlichkeit für eine solche Abweichung mit einer fairen Münzen liegt bei fast 16% – kein Grund misstrauisch zu werden.
Erst nach 30 Millionen Würfen, würde mein Betrug wieder offensichtlich werden. Dann hätte mein Gegenüber im Schnitt 15.000 Mal zu selten Zahl getroffen – eine Abweichung, die mit einer fairen Münze mit einer Wahrscheinlichkeit von 1 zu 46 Millionen vorkommt.
Aber es wird ja wohl Keiner so viele Spiele gegen mich machen. Und wenn doch – nach 30 Millionen Würfen hätte ich durch meinen Betrug immerhin schon 30.000 Euro verdient.
Was aber wenn ich mit meinem Betrugs-Spiel auf ganz großer Masche abräumen will? Millionen Münzwürfe an einer Straßenecke anbieten, ist viel zu aufwendig – ich muss ins Internet und gegen tausende Spieler parallel antreten. Doch da lauert wieder eine ganz neue Gefahr: Verrückte Datensammler könnten abermillionen Würfe protokollieren und mir so doch noch einen Strick drehen. Im Online-Poker haben unter anderem der Online-Poker-Watchdog und Spadebidder zig Millionen Hände untersucht. Sollte das einer bei mir machen, könnte mein Betrug doch wieder auffallen, auch wenn einzelne Spieler nie und nimmer was merken würden.
Aber ich will einfach mal hoffen, das so etwas nicht passiert. Im Falle des Falles könnte ich ja noch etwas seltener betrügen, zum Beispiel nur bei jeden zehntausendsten Wurf. Dann würde es schon rund 3 Milliarden Würfe benötigen, bis mein Betrug auffällt. Und eine so große Datenmenge wird voraussichtlich kein Mensch erfassen.
Der ganz legale Betrug

Ich könnte aber zusätzlich noch auf eine ganz andere Art und Weise Geld verdienen: Ich könnte von meinen Mitspielern eine kleine Gebühr dafür verlangen, dass ich das Spiel überhaupt anbiete und mir die Mühe mache, Münzen zu werfen. 3 Prozent Gebühr pro Wurf klingt nach einem fairen Angebot. Damit müssten die Spieler pro Wurf nur 3 Cent abgeben, und mir würde ganz automatisch Geld in die Kasse gespült.
Pro 100 Würfe würde ich 3 Euro verdienen, ganz unabhängig davon, ob ich betrüge oder nicht.
Nun nehme ich den obigen “versteckten Betrug”, wo ich nur jeden tausendsten Wurf manipuliere. Nach 30 Millionen Würfen hätte ich durch meinen Betrug 30.000 Euro verdient. Aber gleichzeitig hätte ich durch die Spielgebühr schon 900.000 Euro eingenommen.
Aha! Wenn ich – um nicht entdeckt zu werden – so unauffällig manipuliere, bringt mein Betrug im Vergleich kaum noch was ein. Denn durch die Gebühr verdiene ich das Dreißigfache!
Lohnt sich mein Betrug denn dann überhaupt noch? Nur noch rund 3% meiner Einnahmen stammen überhaupt aus meinem Betrug, die restlichen 97% habe ich anständig mit meiner Gebühr verdient.
Im Grunde kann ich dann auch auf meinen Betrug zur Gänze verzichten und gehe nicht das Risiko ein, dass ein verrückter Datensammler zig Millionen meiner Münzwürfe protokolliert und mich des Betruges anprangert.
Klar, wenn ich nur mal fix an einer Straßenecke ein paar Euro verdienen will, ist mein Betrug mit einer manipulierten Münze, die ich möglichst häufig einstreue, immer noch deutlich lukrativer als die Spielgebühr, aber dann kann ich höchstens ein paar hundert Würfe machen, ohne entdeckt zu werden und höchstens ein paar hundert Euro verdienen.
Will ich das ganz große Geld verdienen, bin ich, um unentdeckt zu bleiben, gezwungen so unauffällig zu betrügen, dass ich durch die Spielgebühr deutlich mehr gewinne.
Betrug und Gebühr im Vergleich
Die folgende Tabelle zeigt, wie lange ich mit meinem Betrug unentdeckt durchkomme, wie viel Geld ich bis dahin mit meinem Betrug verdient habe und wie viel Geld ich derweil durch eine 3-prozentige Spielgebühr einnehme.
Die erste Spalte indiziert, bei jedem wievielten Wurf ich mit der manipulierten Münze werfe, die zweite Spalte, wie viele Würfe ich durchführen kann, bevor das Spielergebnis statistisch so sehr von einem fairen Spiel abweicht, dass mein Betrug entdeckt wird2.
| Betruf jeden x-ten Wurf | Würfe bis zur Entdeckung des Betrugs | Gewinn durch Betrug | Gewinn durch Gebühr | Betrugsanteil am Gesamtgewinn |
| 2 | 100 | €50 | €3 | 94,3% |
| 5 | 600 | €120 | €18 | 87,0% |
| 10 | 3.000 | €300 | €90 | 76,9% |
| 20 | 10.000 | €500 | €300 | 62,5% |
| 50 | 60.000 | €1.200 | €1.800 | 40,0% |
| 100 | 300.000 | €3.000 | €9.000 | 25,0% |
| 200 | 1.000.000 | €5.000 | €30.000 | 14,3% |
| 500 | 6.000.000 | €12.000 | €180.000 | 6,3% |
| 1.000 | 30.000.000 | €30.000 | €900.000 | 3,2% |
| 2.000 | 100.000.000 | €50.000 | €3.000.000 | 1,6% |
| 5.000 | 600.000.000 | €120.000 | €18.000.000 | 0,7% |
| 10.000 | 3.000.000.000 | €300.000 | €90.000.000 | 0,3% |
Was hat dieses Beispiel mit Online-Poker zu tun?
Online-Poker ist bei Weitem nicht so simpel wie das hier untersuchte Münzwurf-Spiel. Betrug ließe sich dort deutlich besser verstecken, insbesondere da dem Spieler nicht alle Informationen zu Verfügung stehen. Außerdem gäbe es viele Möglichkeiten, den Betrug zu unterzubringen, zum Beispiel in der Auswahl der Hole-Cards, den Flops, dann und wann ungünstigeren Boards, etwas zu häufig auftretenden Set-Ups oder anderweitig.
Aber ein zentrales Grundprinzip ist identisch mit dem des Münzwurfspiels: Je mehr ein Spieler durch einen Betrug benachteiligt wird, desto deutlicher muss sich dieser Betrug statistisch zeigen und desto größer ist die Wahrscheinlichkeit, dass der Betrug über kurz oder lang entdeckt wird.
Einen Betrug durch manipuliertes Spiel, der sowohl für große Verluste beim Spieler sorgt, als auch langfristig unentdeckt bleibt, gibt es nicht. Das zeigen die obigen Münzwurf-Spiele. Entweder ist ein Betrug so subtil, dass er dem Spieler in seinen Ergebnissen kaum auffällt, oder er ist mit einer realistischen Datenmenge statistisch zu erfassen.
Auch beim Online-Poker nehmen die Anbieter eine Gebühr und auch hier dürfte gelten, dass ein eventueller Betrug durch Manipulation am Ende den Anbietern weit weniger Geld einbrächte als ein sie über die Gebühr ohnehin schon verdienen.
Diese Argumentation kann zwar nicht als Nachweis betrachtet werden, dass Manipulationen nicht stattfinden, aber durchaus als Einschränkung, dass diese Manipulationen, wenn sie denn stattfinden, so subtil sein müssen, dass sie dem Spieler kaum auffallen.
Bislang haben alle Untersuchungen von Online-Poker-Ergebnissen keine Manipulation von Anbieter-Seite aufzeigen können und es haben sich auch noch keine Spieler gefunden, deren Daten Manipulation durch den Anbieter nahelegen. Nach hunderten Milliarden gespielten Online-Poker-Händen, legt allein dies nahe, dass es entweder keine Manipulation durch die Anbieter gibt, oder – und das zeigt dieser Artikel – eine solche Manipulation findet auf einem so niedrigen Level statt, dass kaum ein Spieler nennenswert davon betroffen ist.
Letzteres ist übrigens äußerst unwahrscheinlich. Denn bei jeder Pokerseite müsste zumindest eine gewisse Gruppe von Mitarbeitern in den Betrug eingeweiht sein (irgendwer muss die Algorithmen ja implementieren). Und obwohl in den letzten Jahren unzählige Seiten geschlossen wurden und Mitarbeiter vor die Tür gesetzt wurden, hat bislang noch kein Einziger von derartigen Praktiken berichtet.
1 Münzwurfergebnisse sind binomialverteilt, die Wahrscheinlichkeit lässt sich über diese Formel ausrechnen:
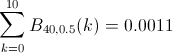
In Excel oder frei verfügbaren Derivaten ist diese Funktion über binomdist integriert.
2 Die Anzahl der Würfe ist (grob gerundet) die Zahl bei der die statistische Abweichung durch den Betrug mit einer Wahrscheinlichkeit von weniger als eins zu einer Million vorkommt und mindestens 5 Standardabweichung vom Erwartungswert einer fairen Münze entfernt liegt.
'
Dieser Artikel erschien auf PokerOlymp am 20.07.2013.

